Rabi振荡
(更新中)
两能级系统到两带系统的rabi振荡。
二能级系统的Rabi振荡
具有耦合的二能级系统
考虑两能级原子,其具有两个能态
两能级间的耦合强度用一个泛指的V代表(V可以是任何形式,不一定是常数)。
哈密顿量可以表示为矩阵形式:
我们定义:
平均能量:
能级间隔:
等效磁场矢量:
哈密顿量可以改写为:
而后面的
频率和能量间有对应关系:
定义两能级间的跃迁频率:
在频率量纲下(将单位1换位
基矢为:
取非对角耦合为正弦驱动
将平均能量位置设为0点(即去掉去掉平均能量),含时哈密顿量为:
旋波近似RWA
采用旋波近似法(RWA)后
RWA是略去微小的高频振荡的一种做法。在这里可以简做如下简要理解:
粒子在基态到激发态跃迁主要过程是吸收光子,反之主要为释放光子。
因此非对角元仅各自仅在
同样,可以按自旋在磁场运动理解,可以改写成一个等效磁场和等效自旋的点乘
可以看到磁场的垂直分量在x-y平面内保持强度按一定角频率旋转。
而自旋在这个旋转磁场下进行拉莫尔进动。通过引入旋转坐标系可以方便的处理这个问题。
在旋转坐标系下研究
引入幺正变换进入旋转坐标系:
以共振驱动为例:
初态为:
可以发现粒子在能级间不断的进行振荡(跃迁)。这便是拉比振荡
非厄米两能带系统Rabi振荡
Ultrafast and anharmonic Rabi oscillations between non-Bloch bands (-Ching Hua Lee& Stefano Longhi)
https://doi.org/10.1038/s42005-020-00417-y
实空间下研究
考虑一个实空间哈密顿量 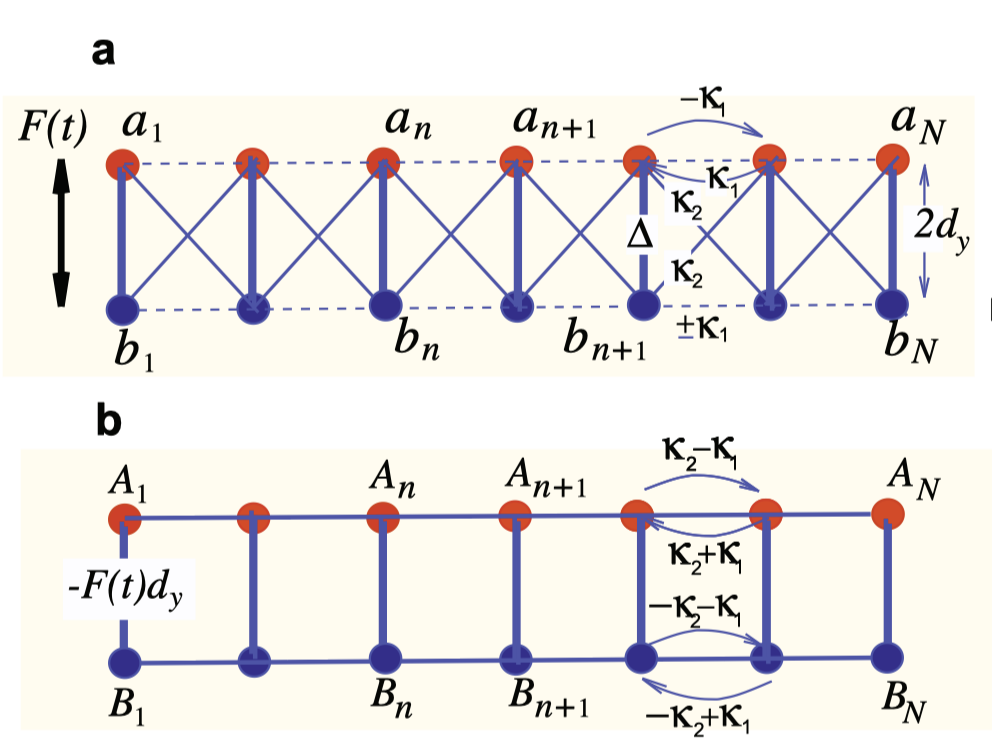
相当于上图a中结构。
通过相似变换对角化:
变换后新基下波函数为
we obtain coupled equations describing the evolution of the amplitude probabilities
Rabi频率正比于有效偶极矢量:
k空间下求解
PBC
在PBC下,k空间哈密顿量为: $$$$
利用量子化的准动量表示为平面波的形式:
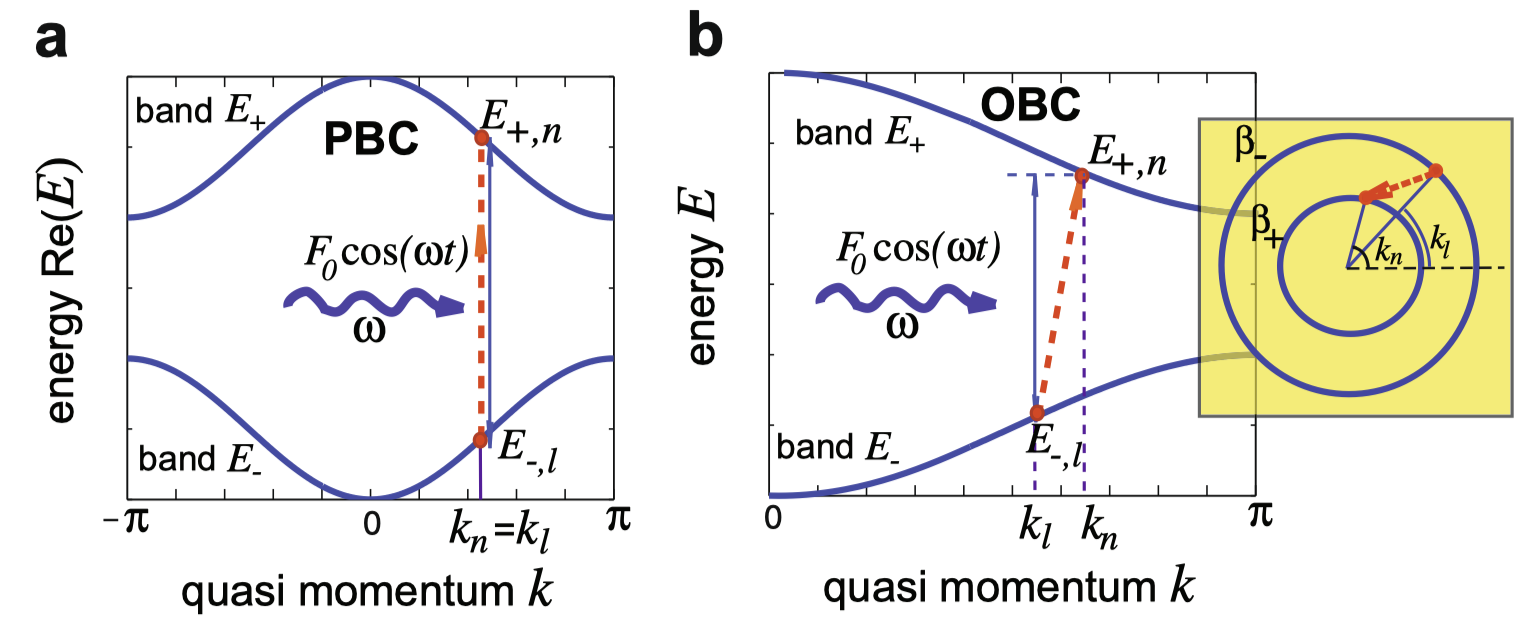
ROs 总是谐波的形式,并且有效偶极矢量总是不变的,没有任何的增强。
OBC
在开边界条件下,没有趋肤效应的波函数是具有Bloch系数(
OBC下的
存在趋肤效应的时,可以通过引入GBZ使得PBC和OBC下的本征态形成一一对应。也就是作如下拓展。
如果叠加系数要在热力学极限中收敛,我们需要存在体-边对应关系,即没有趋肤效应。
对于特定的能量波函数需要在x=0和x=N+1处为0。要使波函数在x=0处消失,需要有至少两个非零特征态的叠加。
为了使它在任意大的N的热力学极限中也在x=N+1时消失,另一个先决条件是两个特征态必须以相同的速度衰减,否则其中一个与另一个相比将小得不能再小,并且不可能在x=N+1时抵消它. 两个特征态以相同的速度衰减的这一要求,仅需要它们的虚动量分量相等,即
在OBC下, 动量不在是一个好量子数,复动量变换可以解释为复规范的相似变换。
在热力学极限中,几乎所有的状态(除了孤立的边缘状态)都是边界态,因此,OBC谱
并且由上个公式也可以得到, 对于同一个能量有:
由此可得:
可见即使
共振频率也与尺寸指数相关,且和